Question

5. Helen, Riley, and Derrick are on a running team. Helen ran 15 1/4 kilometers last week. Riley ran 4 1/12 less kilometers than Helen, and Derrick ran 7 3/8 more kilometers than Riley. If their goal is to run 60 kilometers in total, how much further do they need to run to meet their goal? I

Answer 1

Given in the scenario:

a.) Helen ran 15 1/4 kilometers last week.

b.) Riley ran 4 1/12 less kilometers than Helen.

c.) Derrick ran 7 3/8 more kilometers than Riley.

d.) Their goal is to run 60 kilometers in total.

To be able to determine how much further do they need to run to get 60 kilometers in total, we must first determine how many kilometers did Riley and Derrick run.

We get,

A.)

`\text{Riley: }4(1)/(12)\text{ less kilometers than Helen}`
`\text{ = 15 }(1)/(4)\text{ - 4 }(1)/(12)`

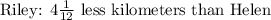
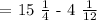
Recall: To be able to subtract mixed numbers, you must first convert them into an improper fraction with a common denominator. The LCM of the two denominators must be their denominator when converted.

The LCM of 4 and 12 is 12. We get,

`\text{ 15 }(1)/(4)\text{ = }\frac{1\text{ + (4 x 15)}}{4}\text{ = }\frac{1\text{ + 60}}{4}\text{ = }(61)/(4)\text{ = }((61)(3))/(12)\text{ = }(183)/(12)`
`4\text{ }(1)/(12)\text{ = }\frac{1\text{ + (4 x 12)}}{12}\text{ = }\frac{1\text{ + 48}}{12}\text{ = }(49)/(12)`

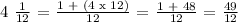
Let's now proceed with the subtraction,

`15(1)/(4)-4(1)/(12)=(183)/(12)\text{ - }(49)/(12)\text{ = }\frac{183\text{ - 49}}{12}\text{ = }(134)/(12)\text{ = }((134)/(2))/((12)/(2))\text{ = }(67)/(6)\text{ or 11}(1)/(6)`

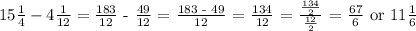
Conclusion: Riley ran 11 1/6 kilometers.

B.)

`\text{Derrick: }7(3)/(8)\text{ more kilometers than Riley}`
`\text{ = 11}(1)/(6)\text{ + 7}(3)/(8)`

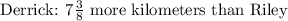
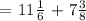
Recall: To be able to add mixed numbers, you must first convert them into an improper fraction with a common denominator. The LCM of the two denominators must be their denominator when converted.

The LCM of 6 and 8 is 24. We get,

`11(1)/(6)\text{ = }\frac{1\text{ + (11 x 6)}}{6}\text{ = }\frac{1\text{ + 66}}{6}\text{ = }(67)/(6)\text{ = }((67)(4))/(24)\text{ = }(268)/(24)`
`7(3)/(8)\text{ = }\frac{3\text{ + (7 x 8)}}{8}=\frac{3\text{ + 56}}{8}=(59)/(8)=((59)(3))/(24)=(177)/(24)`

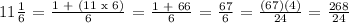
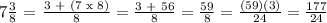
Let's now proceed with the addition,

`11(1)/(6)\text{ + 7}(3)/(8)\text{ = }(268)/(24)\text{ + }(177)/(24)\text{ = }\frac{268\text{ + 177}}{24}\text{ = }(445)/(24)\text{ or 18}(13)/(24)`

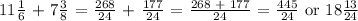
Conclusion: Derrick ran 18 13/24 kilometers.

C.) To be able to determine how much further do they need to run to get 60 kilometers in total, we subtract 60 by the sum of distance the three people ran.

We get,

`\text{ 60 - (15 }(1)/(4)\text{ + 11}(1)/(6)\text{ + 18}(13)/(24))`

The same process that we did, convert all numbers into similar fractions.

The LCM of 4, 6 and 24 is 24. We get,

`15(1)/(4)\text{ = }\frac{1\text{ + }(15\text{ x 4)}}{4}\text{ = }\frac{1\text{ + 60}}{4}\text{ = }(61)/(4)\text{ = }((61)(6))/(24)\text{ = }(366)/(24)`
`11(1)/(6)\text{ = }\frac{1\text{ + (11 x 6)}}{6}\text{ = }\frac{1\text{ + 66}}{6}\text{ = }(67)/(6)\text{ = }((67)(4))/(24)\text{ = }(268)/(24)`
`\text{ 18}(13)/(24)=\text{ }\frac{13+(18\text{ x 24)}}{24}\text{ = }\frac{13\text{ + 432}}{24}\text{ = }(445)/(24)`
`60\text{ = }\frac{60\text{ x 24 }}{24}\text{ = }(1440)/(24)`

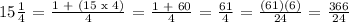
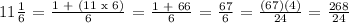
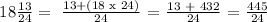
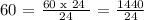
Let's proceed with the operation,

`\text{ 60 - (15 }(1)/(4)\text{ + 11}(1)/(6)\text{ + 18}(13)/(24))\text{ = }(1440)/(24)-((366)/(24)\text{ + }(268)/(24)\text{ + }(445)/(24))`
`\text{ }\frac{1440\text{ - (366 + 268 + 445)}}{24}\text{ = }\frac{1440\text{ - 1079}}{24}`
`\text{ = }(361)/(24)`

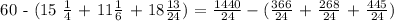
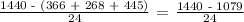
Therefore, they need to run a total of 361/24 kilometers to be able to meet their goal.