First, we need to write our equation in standard form — the y should be on the left- hand - side and the x should be on the right- hand side.
The first step is to subtract x from both sides, doing this we get:
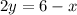
Now we divide both sides of the equation by 2 (this isolates the y on LHS), doing this gives us:
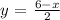
which can also be written as
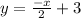
The y-intercept is the point at which the line described by our equation intersects the y-axis. This intersection happens when x = 0; therefore, the y-intercept is
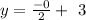

The x-intercept is the point at which the line intersects the x-axis. This happens when y =0; therefore, the x-intercept is
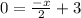
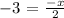

Now we see that the slope of the equation is -1/2 (the coefficient of x ). The y-intercept is y = 3 and the x-intercept is 6.