Question

A wedding planner placed two orders with a flower shop. The first order was for 13 bunches of roses and 4 palms, totaling $487. The second was for 6 bunches of roses and 2 palms, totaling $232. The receipts do not list the item per price. What is the cost of one bunch of roses and one palm?

Answer 1

Let's call X the cost of one bunch of roses and Y the cost of one palm.

Then, the first order was for 13 bunches of roses and 4 palms, totaling $487, so:

13X + 4Y = 487

Additionally, the second order was for 6 bunches of roses and 2 palms, totaling $232, so:

6X + 2Y = 232

Then, solving for Y on the first equation, we get:

`\begin{gathered} 13X+4Y=487 \\ 4Y=487-13X \\ Y=(487-13X)/(4) \\ Y=(487)/(4)-(13)/(4)X \\ Y=121.75-3.25X \end{gathered}`

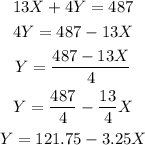
Replacing on the second and solving for X, we get:

`\begin{gathered} 6X+2Y=232 \\ 6X+2(121.75-3.25X)=232 \\ 6X+2\cdot121.75-2\cdot3.25X=232 \\ 6X+243.5-6.5X=232 \\ -0.5X+243.5=232 \\ -0.5X=232-243.5 \\ -0.5X=-11.5 \\ X=(-11.5)/(-0.5) \\ X=23 \end{gathered}`

Then, we can replace the value of X and calculated the value of Y as:

`\begin{gathered} Y=121.75-3.25X \\ Y=121.75-3.25\cdot23 \\ Y=121.75-74.75 \\ Y=47 \end{gathered}`

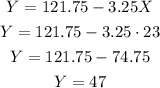
Answer: The cost of one bunch of roses is $23 and the cost of one palm is $47