Question

A bridge AB is to be built across a river. The point C is located 62m from B, and angle A is 80 degrees, angle C is 60 degrees. How long is the bridge

Answer 1

The points A, B, and C form a triangle.

From the given information in the question, the triangle ABC can be drawn to have the following parameters:

Recall the Sine Rule. Applied to the triangle above, the rule is stated as follows:

`(BC)/(\sin A)=(AC)/(\sin B)=(AB)/(\sin C)`

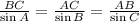
The length of the bridge is AB. Given that the measures of angles A and C, and side BC are known, the following ratio is used to solve:

`(BC)/(\sin A)=(AB)/(\sin C)`

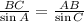
Substituting known values, the length of AB is calculated as follows:

`\begin{gathered} (62)/(\sin80)=(AB)/(\sin60) \\ AB=(62*\sin60)/(\sin80) \\ AB=54.52 \end{gathered}`

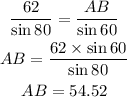
The bridge is 54.52 m long.