Step 1: Lets calculate angle on each hour hand
since the wall clock takes the shape of a cirle
Therefore,
The total angles in a walk clock is 360°
Angle on each hour hand is
There are 12 hour hands on the clock ,
Therefore,
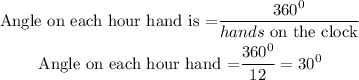
Since the hour hand moved from 5 o'clock to 9 o'clock
It has moved a distance of (9 - 5)= 4 hands on the clock
If each hand on the clock=30°
Therefore,
The angle in degrees moved through 4 hour hands on the clock will be calculated as,
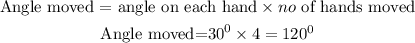
The hour hand of the clock moved from 5 o'clock to 9 o'clock through an angle of 120°