SOLUTION
This is a permutation problem.
a) To find the number of possible two digits codes
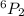
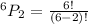
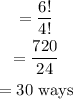
There are 30 possible two-digit codes pattern.
b) To find the number of three digits codes
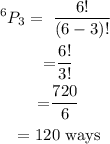
There are 120 possible three-digit codes pattern.
Any other pattern can be calculated using
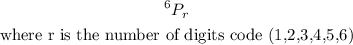
So to predict the number of possible five-digit codes will be:
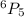
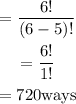
There are 720 different possible five-digit codes