we know that
A cubic equation has zeros at -2, 1, and 3
so
the factors of the cubic equation are
(x+2), (x-1) and (x-3)
Part a
The equation of a polynomial is
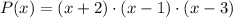
Applying distributive property
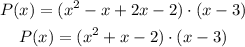
Applying distributive property again
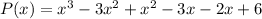
Combine like terms
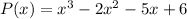
Part b
using a graphing tool
see the attached figure below