Take into account that this is a situation where the source moves presenting the Doppler effect.
In order to determine the wavelength of the sound generatd by the whistle at the observer, first calculate the frequency at the observer by using the following formula:
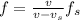
where:
f: frequency at the observer = ?
fo: source frequency = 725 Hz
vs: source speed = 25.2 m/s
v: speed of sound = 345 m/s
replace the previous values of the parameters into the fomrula for f:
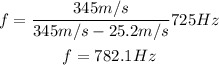
Next, use the following formula to determine the wavelength of the sound at observer, by using the previous result:
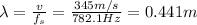
Hence, the wavelength of the sound at the observer is 0.441 m