Question

I need help with this problem it says to find the area of each shaded sector and round to the hundredth place

Answer 1

1330.81 square feet

Explanation:

In the circle, there are two unshaded sectors with central angles 26° and 90°.

The sum of the central angles = 360°.

Therefore, the sum of the central angle of the shaded sectors will be:

`360\degree-(26\degree+90\degree)=244\degree`

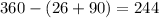
The area of a sector is calculated using the formula:

`A=(\theta)/(360\degree)*\pi r^2\text{ where }\begin{cases}Central\; Angle,\theta=244\degree \\ Radius,r,HK=25ft\end{cases}`

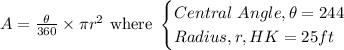
Substitute the values into the formula:

`\begin{gathered} A=(244)/(360)*\pi*25^2 \\ =1330.8136 \\ \approx1330.81\; ft^2 \end{gathered}`

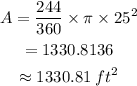
The area of the shaded sector is 1330.81 square feet (rounded to the hundredth place).