Well we just need to do the analise of the function h, so for the first question we need to know what is the value of h when x=0, so if we evaluate we see that
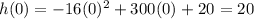
So the first answer is that the start heigth of the rocket is 20.
Now for the second we need to do the derivate and see the critical ponit to know the maximum, we are going to calculate first the derivate, so
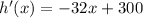
now we need to find the critical ponits so for this, we are going to see when h'(x) = 0, this meand when the derivate is equal to zero, so h'(x) = 0 when
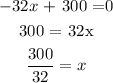
to see if this critical poni is a maximum we need to calculate the secon derivate and see that the second derivate valued in 300/32 is smaller than 0, so
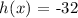
now when x= 300/32 we have that h''(x) is -32 because the second derivate is constant, in this case h''(300/32) < 0, because of this the answer is that 300/32 is the maximum, bur 300/32 = 75/8.
Now for the third question, we need to see the roots of h, so we need to see when h is zero, so for wich values of x we have that h(x) = 0, then

we can solve this with the quadratic equation to solve this kind of equations. This equation is
so we have that
![\begin{gathered} x\text{ = }\frac{-300\text{ }\pm\sqrt[]{300^2\text{ -4(-16)20}}}{2(-16)} \\ x\text{ = }\frac{-300\text{ }\pm\sqrt[]{90000\text{ + 1280}}}{-32} \\ x\text{ = }\frac{-300\text{ }\pm\sqrt[]{91280}}{-32} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/12sxt7lvbzt68s1a16o17vl2l7l73zo1lw.png)
the answer is x = (-300 - v/ 91280)/(-32) or x = (-300 + v/ 91280)/(-32) and this is equal to x = (300 + v/ 91280)/(32) or x = (300 - v/ 91280)/(32) if you prefer. We can also write the answer in a simpler way: x = (75 + v/ 5705)/(8) or x = (75 - v/ 5705)/(8), this is
![x\text{ = }\frac{75\text{ }\pm\sqrt[]{5705}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/3vii4xqfznmd2mg2bscafiwhu6cp7vwsln.png)