Question

Last year, Kevin had $10,000 to invest. he invested some of it in an account that paid 6% simple interest per year, and he invested the rest in an account that paid 10% simple interest per year. after one year, he received a total of $920 in interest. how much did he invest in each account?first account:second account:

Answer 1

Simple interest is represented by the following expression:

`\begin{gathered} I=\text{Prt} \\ \text{where,} \\ I=\text{ interest} \\ P=\text{principal} \\ r=\text{interest rate in decimal form} \\ t=\text{ time (years)} \end{gathered}`

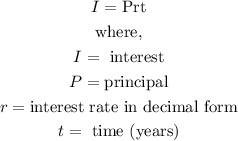
We need to create a system of equations:

Let x be the money invested in the account that paid 6%

Let y be the money invested in the account that paid 10%

So, he received a total of $920 in interest, then:

`920=0.06x+0.1y\text{ (1)}`

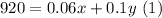
And we know that money invested must add together $10,000:

`x+y=10,000\text{ (2)}`

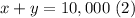
Then, we can isolate y in equation (2):

`y=10,000-x`

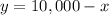
Now, let's substitute y=10,000-x in the equation (1):

`\begin{gathered} 920=0.06x+0.1(10,000-x) \\ 920=0.06x+1000-0.1x \\ 0.1x-0.06x=1,000-920 \\ 0.04x=80 \\ x=(80)/(0.04) \\ x=2,000 \end{gathered}`

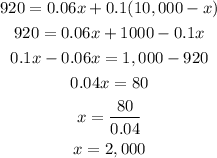
That means, he invested $2,000 in the account that paid 6% simple interest. Now, having x, we are going to substitute x in the second equation (2):

`\begin{gathered} y=10,000-x \\ y=10,000-2,000 \\ y=8,000 \end{gathered}`

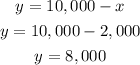
He invested $8,000 in the account that paid 10% simple interest per year.