Question

In the designers proposal, they state that the paths EC and DB each measure 100 feet. They also state that the garden will require 140 feet of hedges. Are their numbers reasonable?

Answer 1

We are given a circle whose diamter is 100 feet. To find out if 140 feet of hedges will fit into it given all the oother dimensions, we will have to calculate the lengths of the chords that correspond to the hedges.

First, let us solve for AE.

`\begin{gathered} chord=2r\sin\theta \\ \\ AE=100\sin50 \\ AE=76.6 \end{gathered}`

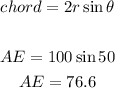
We used θ = 50 degrees because we know that the measurement of the arc is equal to the measurement of the central angle.

Now, to solve for the length of ED, we need to find out the measurement of the central angle that subtend it.

Segments AD and EC intersect, thus the following equation must be true for the angles that they form and the arcs that they subtend:

`\begin{gathered} m\angle EXA=(1)/(2)(m\hat{AE}+m\hat{DC}) \\ \\ 70=(1)/(2)(50+m\hat{DC}) \\ \\ 140=(50+m\hat{DC}) \\ \\ 90=m\hat{DC} \end{gathered}`

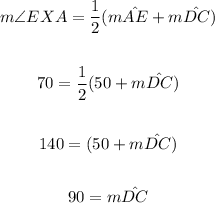
Again, using the formula for finding the length of a chord, we can now solve for the length of ED.

`\begin{gathered} chord=2r\sin(\theta) \\ \\ ED=100\sin90 \\ ED=100 \end{gathered}`

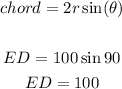
Finally, we need to calculate the length of BC. But we know that BC = ED because the diameters meet at a 90-degree angle and so the chords that they subtend are all congruent. You may also think of ∠BYC as being vertical to ∠EYD. So BC should be equal to ED either way. BC = 100

So the total length of the hedges is:

`\begin{gathered} AE+ED+BC \\ =76.6+100+100 \\ =276.6ft \end{gathered}`

Therefore, the numbers given by the designers are not reasonable. 140 feet is too short for the hedges.