SOLUTION:
Step 1:
In this question, we have the following:
Step 2:
Part A:
The function that models the population of Star, ID in years since 2000 is:
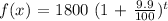
Part B :
Use your function to predict the population of Star, ID in 2050
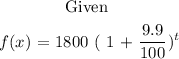
The year 2050 means that t= 50, we have that:
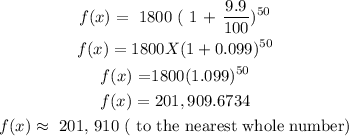
Part C:
The function:
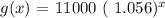
models the population of Eagle, ID in years (x) since 2000.
Which city is growing faster? How do you know?
Answer:
From this equation, we can see that the growth rate is 5.6% annually.
Comparing this, with the initial function:
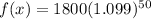
We can see that the annual growth rate of f(x) is 9.9 %
CONCLUSION:
The population of Star ID, with the function, g (x) has a faster growth rate.