Question

Question 37?Find the indicated function and state its domain in interval notation?

Answer 1

Given the functions:

`\begin{gathered} f(x)=-\sqrt[]{x-3} \\ g(x)=3x \end{gathered}`

You need to multiply them, in order to find:

`(f\cdot g)(x)`

Then, you get:

`\begin{gathered} (f\cdot g)(x)=(-\sqrt[]{x-3})(3x) \\ (f\cdot g)(x)=-3x\sqrt[]{x-3} \end{gathered}`

In order to find the Domain, you need to remember that the Domain of a Radical Function are those input values (x-values) for which the Radicand is positive. Then, in this case, you need to set up that:

`x-3\ge0`

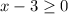
Now you have to solve for "x":

`x\ge3`

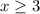
Therefore:

`Domain\colon\lbrack3,\infty)`

Hence, the answer is:

`\begin{gathered} (f\cdot g)(x)=-3x\sqrt[]{x-3} \\ \\ Domain\colon\lbrack3,\infty) \end{gathered}`