Question

If A={a,c} and B={d,g,w} then complete the Following:a. Find AxBb. Find n(AxB)c. write a multiplication equation involving numerals related to the parts in (a) and (b)...a. AxB = {____} Type an ordered pair. Use commas to separate answers as needed

Answer 1

Given the two sets:

`\begin{gathered} A=\mleft\lbrace a,c\mright\rbrace \\ B=\mleft\lbrace d,g,w\mright\rbrace \end{gathered}`

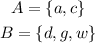
we can write the product set of A and B in the following form:

`AxB=\mleft\lbrace(a,d\mright),(a,g),(a,w),(c,d),(c,g),(c,w)\}`

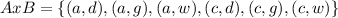
next, we have that the number of elements in A is 2 and the number of elements in B is 3, then, we have:

`n(AxB)=2\cdot3=6`

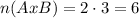
finally, the equation that involves the numerals of the previous parts is:

`n(AxB)=n(A)\cdot n(B)`

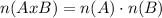
where n(A) and n(B) represents the number of elements in A and B respectively.