Question

A circle has a center point at the coordinates P(3,0) with a diameter line RT where R has the coordinates (-47,25).What is the Coordinates Of T

Answer 1

Given: A circle has a center point at the coordinates P(3,0) with a diameter line RT where R has the coordinates (-47,25).

Required: To determine the coordinates of T.

Step-by-step explanation: The given circle is-

Let the coordinates of T be (x,y). Then the center of a circle is divided by the diameter in the ratio of 1:1. The section formula for a point (x,y) dividing a line segment in the ratio of 1:1 is-

`\begin{gathered} x=((x_1+x_2))/(2), \\ y=((y_1+y_2))/(2) \end{gathered}`

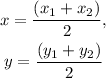
Hence, for the given line RT, point P divided RT in 1:1. Thus-

`\begin{gathered} 3=(-47+x)/(2), \\ 0=(25+y)/(2) \end{gathered}`

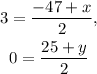
Further solving for x and y as-

`\begin{gathered} x=6+47 \\ \Rightarrow x=53 \\ and\text{ }y=-25 \end{gathered}`

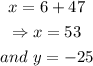
Final Answer: The coordinates of T are (53,-25).