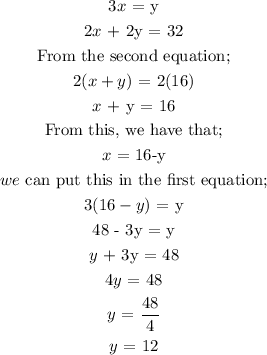Question

Given the figure, find the value of y for which the quadrilateral must be a parallelogram

Answer 1

For the figure to be a parallelogram, then y must be equal to 12

Here, we want to get the value of y for which the the quadilateral must be a parallelogarm

Mathematically, the diagonals of a parallelogarm bisects each other

That means the lengths on either sides are equal

Mathematically, we can get two equations as follows;

`\begin{gathered} 3x\text{ = y} \\ 2x\text{ + 2y = 32} \\ \text{From the second equation;} \\ 2(x+y)\text{ = 2(16)} \\ x\text{ + y = 16} \\ \text{From this, we have that;} \\ x\text{ = 16-y} \\ we\text{ can put this in the first equation;} \\ 3(16-y)\text{ = y} \\ 48\text{ - 3y = y} \\ y\text{ + 3y = 48} \\ 4y\text{ = 48} \\ y\text{ = }(48)/(4) \\ y\text{ = 12} \end{gathered}`