Question

Which describes a line passing through (3,3) that is perpendicular to the line described by y=3/5x+2 ?

Answer 1

Given:

Point (3,3)

The equation of the line,

`y=(3)/(5)x+2`

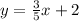
To find the equation of the line that passes through (3,3) and is perpendicular to the line:

The perpendicular slope is,

`m=-(5)/(3)`

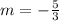
Using the point-slope formula,

`\begin{gathered} y-y_1=m(x-x_1) \\ y-3=-(5)/(3)(x-3) \\ y=-(5)/(3)x+5+3 \\ y=-(5)/(3)x+8 \end{gathered}`

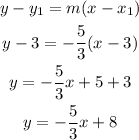
Hence, the equation of the line is,

`y=-(5)/(3)x+8`

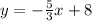
Let us find the intercepts.

When x=0, we get y=8

So, the y-intercept is (0,8).

When y=0, we get

`\begin{gathered} -(5)/(3)x+8=0 \\ (5)/(3)x=8 \\ x=(24)/(5) \\ x=4.8 \end{gathered}`

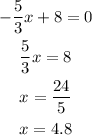
So, the x-intercept is (4.8,0).

Hence, the correct option which satisfies the equation of the line is D (last option).