Question

Nguyen deposited $35 in a bank account earning 14% interest, compounded annually. How much interest will he earn in 72 months?

Answer 1

Given:

a.) Nguyen deposited $35 in a bank account.

b.) It earns 14% interest.

To be able to determine how much interest will he earn in 72 months, the following formula will be used for Compound Interest:

`\text{ Interest Earned = P(1 + }((r)/(100))/(n))^(nt)\text{ - P}`

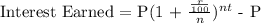
Where,

P = Principal amount

r = Interest rate

n = No. of times the interest is compounded = annually = 1

t = Time in years = 72 months = 72/12 = 6 Years

We get,

`\text{ Intereset Earned = (35)(1 + }((14)/(100))/(1))^((1)(6))\text{ - 35}`
`\text{ = (35)(1 + }0.14)^6\text{ - 35}`
`\text{ = (35)(}1.14)^6\text{ - 35}`
`\text{ = (35)(}2.19497262394)^{}\text{ - 35}`
`\text{ = 76.82404183776 - 35}`
`\text{ = 41.82404183776 }\approx\text{ 41.82}`
`\text{ Interest Earned = \$41.82}`

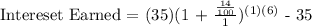
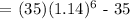
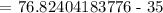
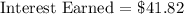
Therefore, the interest he will be earning is $41.82