Question

I need help with homework . BC=5, angle A=25 degree.

Answer 1

AC = 2.332

AB = 5.517

Step-by-step explanation:

Given:

BC = 5.

Angle B = 25 degree.

Angle C = 90 degree.

The objective is to find AC and AB.

By the trigonometric functions, Consider AB as hypotenuse, AC as opposite and BC as adjacent.

Then, the relationship between opposite (AC) and adjacent (BC) cnbe calculated by trigonometric ratio of tan theta.

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan 25^0=(AC)/(5) \\ AC=\tan 25^0\cdot5 \\ AC=2.332 \end{gathered}`

Now, the length AB can be calculated by Pythagorean theorem,

`\begin{gathered} AB^2=AC^2+BC^2 \\ AB^2=2.332^2+5^2 \\ AB^2=5.436+25 \\ AB^2=30.436 \\ AB=\sqrt[]{30.436} \\ AB=5.517 \end{gathered}`

Let's check the value using trigonometric ratios.

For the relationship of opposite and hypotenuse use sin theta.

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \sin 25^0=(2.332)/(y) \\ y=(2.332)/(\sin 25^0) \\ y=5.517 \end{gathered}`

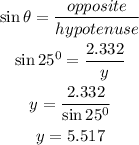
Thus both the answers are matched.

Hence, the length of the side AC = 2.332 and the length of the side AB = 5.517.