Question

1. The figure shows the regular triangular pyramid SABC. The base of the pyramid has an edge AB = 6 cm and the side wall has an apothem SM = √15 cm. Calculate the pyramid: 1) the base elevation AM; 2) the elevation SO; 3) the area of the base; 4) the area of the side surface; 5) the total surface area; 6) volume.

Answer 1

Given:

• AB = 6 cm

,

• SM = √15 cm

Let's solve for the following:

• 1) the base elevation AM.

Given that we have a regular triangular pyramid, the length of the three bases are equal.

AB = BC = AC

BM = BC/2 = 6/2 = 3 cm

To solve for AM, which is the height of the base, apply Pythagorean Theorem:

`\begin{gathered} AM=√(AB^2-BM^2) \\ \\ AM=√(6^2-3^2) \\ \\ AM=√(36-9) \\ \\ AM=√(27) \\ \\ AM=5.2\text{ cm} \end{gathered}`

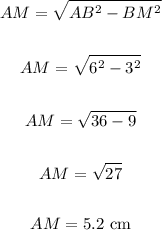
The base elevation of the pyramid is 5.2 cm.

• (2)., The elevation SO.

To find the elevation of the pyramid, apply Pythagorean Theorem:

`SO=√(SM^2-MO^2)`

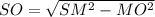
Where:

SM = √15 cm

MO = AM/2 = 5.2/2 = 2.6 cm

Thus, we have:

`\begin{gathered} SO=\sqrt{(√(15))^2-2.6^2} \\ \\ SO=√(15-6.76) \\ \\ SO=2.9\text{ cm} \end{gathered}`

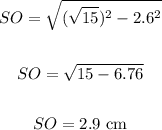
Length of SO = 2.9 cm

• (3). Area of the base:

To find the area of the triangular base, apply the formula:

`A=(1)/(2)*BC*AM`

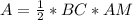
Thus, we have:

`\begin{gathered} A=(1)/(2)*6^*5.2 \\ \\ A=15.6\text{ cm}^2 \end{gathered}`

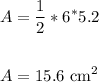
The area of the base is 15.6 square cm.

• (4). Area of the side surface.

Apply the formula:

`SA=(1)/(2)*p*h`

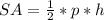
Where:

p is the perimeter

h is the slant height, SM = √15 cm

Thus, we have:

`\begin{gathered} A=(1)/(2)*(6*3)*√(15) \\ \\ A=34.86\text{ cm}^2 \end{gathered}`

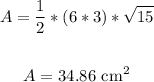
• (5). Total surface area:

To find the total surface area, apply the formula:

`TSA=base\text{ area + area of side surface}`

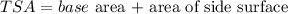
Where:

Area of base = 15.6 cm²

Area of side surface = 34.86 cm²

TSA = 15.6 + 34.86 = 50.46 cm²

The total surface area is 50.46 cm²

• (6). Volume:

To find the volume, apply the formula:

`V=(1)/(3)*area\text{ of base *height}`

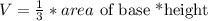
Where:

Area of base = 15.6 cm²

Height, SO = 2.9 cm

Thus, we have:

`\begin{gathered} V=(1)/(3)*15.6*2.9 \\ \\ V=15.08\text{ cm}^3 \end{gathered}`

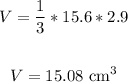
The volume is 15.08 cm³.

ANSWER:

• 1.) 5.2 cm

,

• 2.) 2.9 cm

,

• 3.) 15.6 cm²

,

• 4.) 34.86 cm²

,

• (5). 50.46 cm²

,

• 6). 15.08 cm³.