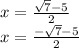Answer: x =
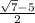
x =

Step-by-step explanation:
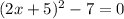
Add 7 to both sides of the equation.

Subtracting 7 from itself leaves 0.
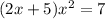
Take the square root of both sides of the equation.

Subtract 5 from both sides of the equation.
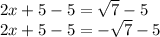
Subtracting 5 from itself leaves 0.

Subtract 5 from
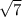 .
.
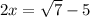
Subtract 5 from
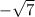 .
.
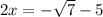
Divide both sides by 2.
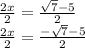
Dividing by 2 undoes the multiplication by 2.