Question

In a certain fraction, the denominator is 3 less than the numerator. If 1 is added to both the numerator and denominator, the resulting fraction is equal to 10/7 Find the original fraction.

Answer 1

The original fraction has a denominator that is 3 less than the numerator. If we define the numerator as x, then the denominator is x-3, and the fraction can be written as x/(x-3).

If 1 is added both to the numerator and denominator, the resulting fraction is equal to 10/7.

Then, we can write:

`\begin{gathered} (x+1)/((x-3)+1)=(10)/(7) \\ (x+1)/(x-2)=(10)/(7) \\ 7(x+1)=10(x-2) \\ 7x+7=10x-20 \\ 7x-10x=-20-7 \\ -3x=-27 \\ x=(-27)/(-3) \\ x=9 \end{gathered}`

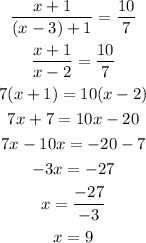
With the value of x, we can replace it in the fraction and know the value of it:

`(x)/(x-3)=(9)/(9-3)=(9)/(6)=(3)/(2)`

Answer: The fraction is 9/6, that can be simplified to 3/2 or 1.5.