Answer:
Step-by-step explanation:
For Blue Car:
Distance = 33 & 1/2 miles
Gasoline = 1 & 1/4 gallons
For Red Car:
Distance = 22 & 2/5 miles
Gasoline = 4/5 gallon
To determine the rate unit rate for miles per gallon for each car, we use the following formula:
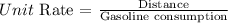
First, we find the unit rate for blue car:
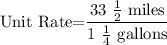
Convert mixed numbers to improper fractions: 33 & 1/2 = 67/2 and 1 & 1/4 = 5/4

Next, we find the unit rate for red car:
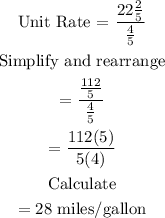
Therefore, the car that could travel the greater distance on 1 gallon of gasoline is the red car.