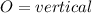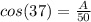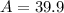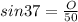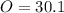Answer:
a.
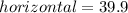 m/s
m/s
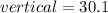 m/s
m/s
b.
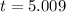
c.
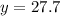
Step-by-step explanation:
Lets write down what we were given.
Angle = 37°
Initial Velocity = 50 m/s
Displacement in x direction = 200 m
Take note:
I am having some trouble with the theta symbol so let theta =
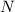
Lets do question C first.
We know that time is equal to
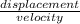 aka
aka
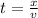 .
.
 ₀ₓ
₀ₓ
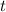 ⇒
⇒
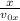 ⇒
⇒
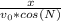
Now substitute the expression for t into the equation for the position.
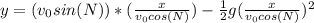
Rearranging terms, we have
![y=(tan(N)*x)-[(g)/(2(v_(0)cos(N))^(2) ) ]x^(2)](https://img.qammunity.org/2023/formulas/physics/college/6f1a4zypwjg2ni072efm8y4o4lasqshzwz.png)
Now lets substitute our numbers in for the variables. Then simplify.
![y=(tan37*200)-[(9.81)/(2(50*cos37)^(2) ) ]200^(2)](https://img.qammunity.org/2023/formulas/physics/college/sruifmqcggkdf885zkzpkl470vknt6rlmg.png)
![y=150.7108-[(9.81)/(2(50*cos37)^(2) ) ]200^(2)](https://img.qammunity.org/2023/formulas/physics/college/fikzso07ftnjwu3wxpku6ov8h1y7n1vqdv.png)
![y=150.7108-[0.0030761]200^(2)](https://img.qammunity.org/2023/formulas/physics/college/lha3ayszg72rlo198pcvv1b76g5ehsmq6f.png)
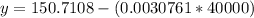
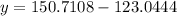
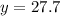
Now lets do question B.
Lets steal this from the last question.
We know that time is equal to
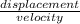 aka
aka
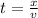 .
.
 ₀ₓ
₀ₓ
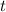 ⇒
⇒
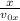 ⇒
⇒
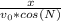
Now substitute the expression for t into the equation for the position.
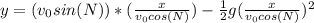
We can substitute
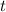 for
for
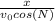
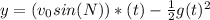
We can rewrite the equation as
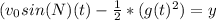
Now lets substitute our numbers in for the variables.
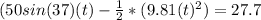
After some painful algebra and factoring we get
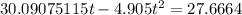
Subtract
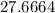 from both sides.
from both sides.
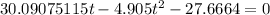
Use the quadratic formula to find the solutions.
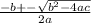
After some more painful algebra we get
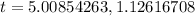
1.126 does not make any sense so.
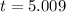
Finally lets do question A.
Lets draw a triangle. We have the velocity which is the hypotenuse and we have the angle. From there we can solve for the opposite and adjacent sides.
Let
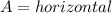 and
and