Question

Find the area of the composite figure.

Answer 1

The Area of the composite figure would be 76.26 in^2

Explanation:

According to the Figure Given:

Total Horizontal Distance = 14 in

Length = 6 in

To Find :

The Area of the composite figure

Solution:

Firstly we need to find the area of Rectangular part.

So We know that,

`\boxed{ \rm \: Area \: of \: Rectangle = Length×Breadth}`

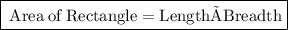
Here, Length is 6 in but the breadth is unknown.

To Find out the breadth, we’ll use this formula:

`\boxed{\rm \: Breadth = total \: distance - Radius}`

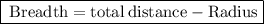
According to the Figure, we can see one side of a rectangle and radius of the circle are common, hence,

`\longrightarrow\rm \: Length \: of \: the \: circle = Radius`

• Since Length = 6 in ;

`\longrightarrow \rm \: 6 \: in = radius`

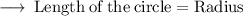
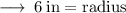
Hence Radius is 6 in.

So Substitute the value of Total distance and Radius:

• Total Horizontal Distance= 14
• Radius = 6

`\longrightarrow\rm \: Breadth = 14-6`

`\longrightarrow\rm \: Breadth = 8 \: in`

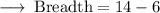
Hence, the Breadth is 8 in.

Then, Substitute the values of Length and Breadth in the formula of Rectangle :

• Length = 6
• Breadth = 8

`\longrightarrow\rm \: Area \: of \: Rectangle = 6 * 8`

`\longrightarrow \rm \: Area \: of \: Rectangle = 48 \: in {}^(2)`

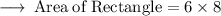
Then, We need to find the area of Quarter circle :

We know that,

`\boxed{\rm Area_((Quarter \; Circle) ) = \cfrac{\pi{r} {}^(2) }{4}}`

Now Substitute their values:

• r = radius = 6
• π = 3.14

`\longrightarrow\rm Area_((Quarter \; Circle) ) = \cfrac{3.14 * 6 {}^(2) }{4}`

Solve it.

`\longrightarrow\rm Area_((Quarter \; Circle) ) = \cfrac{3.14 * 36}{4}`

`\longrightarrow\rm Area_((Quarter \; Circle) ) = \cfrac{3.14 * \cancel{{36} } \: ^(9) }{ \cancel4}`

`\longrightarrow\rm Area_((Quarter \; Circle)) =3.14 * 9`

`\longrightarrow\rm Area_((Quarter \; Circle) ) = 28.26 \: {in}^(2)`

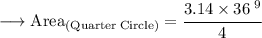
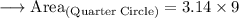
Now we can Find out the total Area of composite figure:

We know that,

`\boxed{ \rm \: Area_((Composite Figure)) =Area_((rectangle))+ Area_( (Quarter Circle))}`

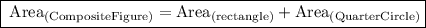
So Substitute their values:

• 
  `\rm Area_((rectangle))` = 48
• 
  `\rm Area_((Quarter Circle))` = 28.26

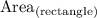`\longrightarrow \rm \: Area_((Composite Figure)) =48 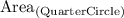+ 28 .26`

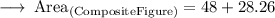
Solve it.

`\longrightarrow \rm \: Area_((Composite Figure)) =\boxed{\tt 76.26 \:\rm in {}^(2)}`

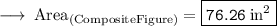
Hence, the area of the composite figure would be 76.26 in² or 76.26 sq. in.

`\rule{225pt}{2pt}`

I hope this helps!