Question

Jose applies a force of 20 N North, Johnny applies a force of 10 N West and Janie applies a force of 25 N south on a heavy dresser. Find the resultant force on the dresser.

Answer 1

Resultant force of the given forces: approximately
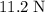`11.2\; {\rm N}` at approximately
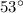`53^(\circ)` west of south.

Step-by-step explanation:

The resultant force of these forces will be:

• 
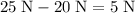  `25\; {\rm N} - 20\; {\rm N} = 5\; {\rm N}` to the south (the
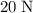  `20\; {\rm N}` force to the north partially balances the
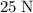  `25\; {\rm N}` force to the south), and
• 
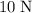  `10\; {\rm N}` to the west.

Refer to the diagram attached. The resultant
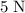`5\; {\rm N}` force to the south and the
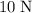`10\; {\rm N}` force to the west are perpendicular to each other, forming the two legs of a right triangle. The hypotenuse of this right triangle will be the net effect of these two forces.

Apply Pythagorean's Theorem on this triangle to find the magnitude of this net effect:

`\begin{aligned}(\text{length of hypotenuse}) &= \sqrt{10^(2) + 5^(2)} \approx 11.2\end{aligned}`.

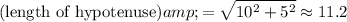Hence, the magnitude of this net effect will be approximately
`11.2\; {\rm N}`.

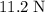Let
`\theta` denote the angle between this resultant force and west. In this right triangle:

`\begin{aligned} \tan(\theta) &= \frac{(\text{opposite})}{(\text{adjacent})} \\ &= \frac{5\; {\rm N}}{10\; {\rm N}} \\ &= (1)/(2)\end{aligned}`.

`\begin{aligned} \theta &= \arctan\left((1)/(2)\right) \approx 27^(\circ)\end{aligned}`.

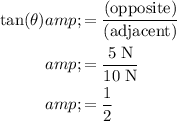Hence, the angle between this resultant force and south will be approximately
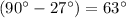`(90^(\circ) - 27^(\circ)) = 63^(\circ)`. This resultant force will be at approximately
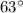`63^(\circ)` west of south.