1 Answer

Poovaraj · Answer 1 · 2023-09-25T19:53:15+0000

Answer:

Area of the shaded region is 104.96 m².

Step-by-step Step-by-step explanation:

Firstly, finding the area of circle with radius 8 cm by substituting the values in the formula :

${:\implies{\tt{A_((Circle)) = \pi {r}^(2)}}}$

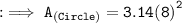
${:\implies{\tt{A_((Circle)) = 3.14{(8)}^(2)}}}$

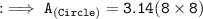
${:\implies{\tt{A_((Circle)) = 3.14{(8 * 8)}}}}$

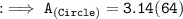
${:\implies{\tt{A_((Circle)) = 3.14{(64)}}}}$

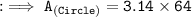
${:\implies{\tt{A_((Circle)) = 3.14 * 64}}}$
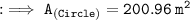
${:\implies{\tt{A_((Circle)) = 200.96 \: {m}^(2) }}}$

Hence, the area of circle is 200.96 m².

$\begin{gathered}\end{gathered}$

Secondly, finding the area of rectangle with length and breadth by substituting the values in the formula :

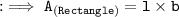
${:\implies{\tt{A_((Rectangle)) = l * b}}}$

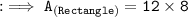
${:\implies{\tt{A_((Rectangle)) = 12 * 8}}}$

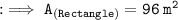
${:\implies{\tt{A_((Rectangle)) = 96 \: {m}^(2)}}}$

Hence, the area of rectangle is 96 m².

$\begin{gathered}\end{gathered}$

Now, finding the area of shaded region by substituting the values in the formula :

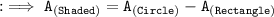
${:\implies{\tt{A_((Shaded)) = A_((Circle)) - A_((Rectangle))}}}$

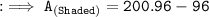
${:\implies{\tt{A_((Shaded)) = 200.96 - 96}}}$

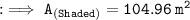
${:\implies{\tt{A_((Shaded)) = 104.96 \: {m}^(2)}}}$

Hence, the area of shaded region is 104.96 m².

$\rule{300}{2.5}$

Please log in or register to add a comment.