Final Answer:
The function that shows a non-differentiable point due to a vertical tangent is f(x) = |x|.
Step-by-step explanation:
The function f(x) = |x| exhibits a non-differentiable point at x = 0 due to a vertical tangent. To understand why, we need to examine the definition of the derivative. The derivative of a function at a point represents the slope of the tangent line at that point. For a function to be differentiable at a certain point, the slope of the tangent line must exist and be unique.
In the case of f(x) = |x|, when x > 0, the function is given by f(x) = x, and when x < 0, the function is f(x) = -x. At x = 0, these two branches meet, and the slope of the tangent line on either side is different. As a result, the derivative at x = 0 does not exist. This is visually represented by a vertical tangent line at the point of intersection.
Mathematically, we can express this by calculating the left-hand and right-hand derivatives at x = 0. The left-hand derivative (from the negative side) is
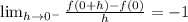 ,
,
and the right-hand derivative (from the positive side) is
 .
.
Since these two values are not equal, the derivative at x = 0 does not exist, indicating a non-differentiable point with a vertical tangent.