Answer:
D. x = 6
Explanation:
Given equation:
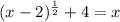
Subtract 4 from both sides:
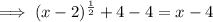
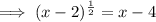
Square both sides:
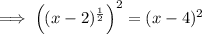
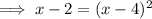
Expand the brackets on the right side:
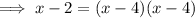
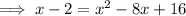
Subtract x from both sides:
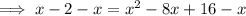
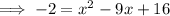
Add 2 to both sides:
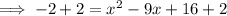
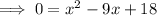
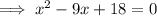
Factor the left side of the equation:
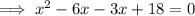
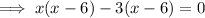
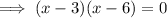
Apply the zero-product property:
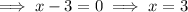
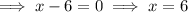
Therefore, the solutions of the quadratic equation are:

Input both solutions into the original equation to check their validity:
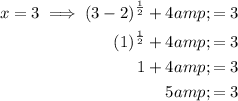
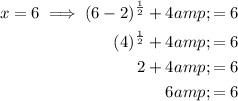
Therefore, the only valid solution to the given equation is x = 6.