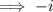Question

Question 2(Multiple Choice Worth 2 points)

(01.06 MC)
Simplify 31.
1
0-1
-1

Answer 1

`-i`

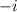
Explanation:

Imaginary numbers

Since there is no real number that squares to produce -1, the number
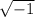`√(-1)` is called an imaginary number, and is represented using the letter
`i`.

Given expression:

`i^(31)`

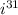
Rewrite 31 as 30 + 1:

`\implies i^(30+1)`

`\textsf{Apply exponent rule} \quad a^(b+c)=a^b \cdot a^c:`

`\implies i^(30) \cdot i^1`

`\implies i^(30)i`

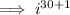
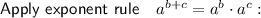
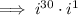
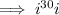
Rewrite 30 as 2 · 15:

`\implies i^((2 \cdot 15))i`

`\textsf{Apply exponent rule} \quad a^(bc)=(a^b)^c:`

`\implies \left(i^2\right)^(15)i`

`\textsf{Apply\:imaginary\:number\:rule}\quad \:i^2=-1:`

`\implies \left(-1\right)^(15)i`

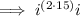
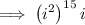
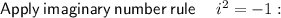
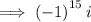
As -1 to the power of an odd number is -1:

`\implies -1 \cdot i`

`\implies -i`