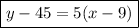Question

A manager measured the number of goods, y, that his company produced in a hours. The

company produces goods at a rate of 5 per hour. At hour 9, the company had produced 45
goods.
Which equation, in point-slope form, correctly represents the goods produced by the company
after x hours?
Oy-45 = 5(x-9)
Oy+9= 5(x +45)
Oy 45= 5(x + 9)
Oy-9=5(x - 45)

Answer 1

`y-45=5(x-9)`

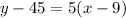
Explanation:

Definition of the variables:

• y = total number of goods produced.
• x = time in hours.

Given information:

• The company produces goods at a rate of 5 per hour.
• At hour 9, the company had produced 45 goods.

As the rate of change is constant and linear, the rate of change is the slope of the line. Therefore, the slope is 5.

At hour 9 (x-value) the company had produced 45 (y-value) goods. Therefore, this can be represented by the point (9, 45).

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Substitute the found slope and point into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-45=5(x-9)`

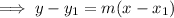
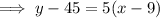
Therefore, the equation that correctly represents the goods produced by the company after x hours is:

`\boxed{y-45=5(x-9)}`