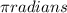For this exercise you need to use the following formula:
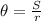
Where θ is the Central angle in radians, "S" is the arc length and "r" is the radius of the circle.
In this case, you can identify that:
![\begin{gathered} S=8\pi cm \\ r=8\operatorname{cm} \end{gathered}]()
Knowing these values, you can substitute them into the formula and then evaluate, in order to find the measure of the Central angle in radians. This is:
![\begin{gathered} \theta=\frac{8\pi cm}{8\operatorname{cm}} \\ \\ \theta\approx\pi radians \end{gathered}]()
The answer is: