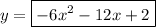Question

Please help 100 points

Answer 1

• y = - 6x² - 12x + 2

======================

Given

• Vertex of parabola = (- 1,8),
• Point on the graph = (0, 2).

To find

• The equation of the parabola in standard form.

Solution

We can represent the quadratic equation in vertex or standard forms.

Vertex form:

• y = a(x - h)² + k, where (h, k) is the vertex, a- coefficient

Standard form:

• y = ax² + bx + c, where a and b are coefficients and c- constant

Use the vertex form with given coordinates of the vertex:

• y = a(x - (-1))² + 8 ⇒
• y = a(x + 1)² + 8

Use the other point to find the value of a:

• 2 = a(0 + 1)² + 8
• 2 = a + 8
• a = - 6

The equation is:

• y = - 6(x + 1)² + 8

Convert it to standard form:

• y = - 6x² - 12x - 6 + 8
• y = - 6x² - 12x + 2

Answer 2

`y=-6x^2-12x+2`

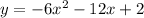
Explanation:

Vertex form of a quadratic equation:

`y=a(x-h)^2+k`

where (h, k) is the vertex.

Given:

• Vertex = (-1, 8)
• Point on the curve = (0, 2)

Substitute the given values into the vertex formula and solve for a:

`\implies 2=a(0-(-1))^2+8`

`\implies 2=a(1)^2+8`

`\implies 2=a+8`

`\implies a=-6`

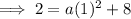
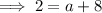
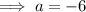
Substitute the vertex and the found value of a into the vertex formula, then expand to standard form:

`\implies y=-6(x-(-1))^2+8`

`\implies y=-6(x+1)^2+8`

`\implies y=-6(x^2+2x+1)+8`

`\implies y=-6x^2-12x-6+8`

`\implies y=-6x^2-12x+2`

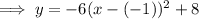
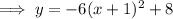
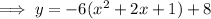
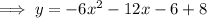
Therefore, the quadratic function in standard form whose graph has the given characteristics is:

`y=\boxed{-6x^2-12x+2}`