Answer:
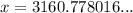
Explanation:
Given logarithmic equation:
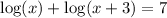
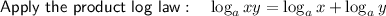
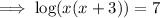


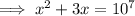
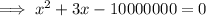
Solve the quadratic equation by using the quadratic formula.
Quadratic Formula
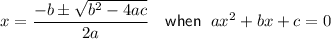
Therefore:

Substitute the values of a, b and c into the quadratic formula:
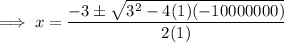

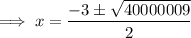
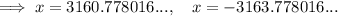
As logs of negative numbers cannot be taken, the only valid solution is:
