Question

Box #1 options is: A.true B.false

Box #2 options are: A.true B.false
Box #3 options are: A.enough B.not enough

Answer 1

Answers:

1. false
2. true
3. not enough

=======================================================

Step-by-step explanation:

Let's say the claim is
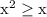`\text{x}^2 \ge \text{x}` true for any real number x. It certainly works for things like x = 5 and x = 27.

A counter-example to show this isn't true is to use x = 0.5

So,

`\text{x}^2 \ge \text{x}\\\\0.5^2 \ge 0.5\\\\0.25 \ge 0.5\\\\`

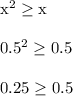
The last statement is false, which thereby proves the original claim doesn't work for x = 0.5; by extension, the overall claim of that inequality working for any real number is false.

As you can see, all we need is one counter-example to contradict the claim to prove it false.

Unfortunately one single example is not enough evidence to prove a claim true. Think of it like saying "it's much easier to knock down a sand castle than to build it up".

Instead, we need to use a set of clearly laid out statements and reasons based on previously established theorems.