Answer:
b) 26%
Explanation:
If a continuous random variable X is normally distributed with mean μ and variance σ², it is written as:
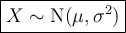
Given:
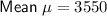
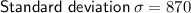
Therefore, if the weights of the cars passing over the bridge are normally distributed:
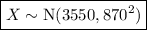
where X is the weight of the car.
To find the approximate probability that the weight of a randomly-selected car passing over the bridge is less than 3000 pounds, find
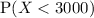 .
.
Calculator input for "normal cumulative distribution function (cdf)":
- Upper bound: x = 3000
- Lower bound: x = –9999...
- μ = 3550
- σ = 870
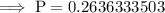
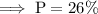
Therefore, the approximate probability that the weight of a randomly-selected car passing over the bridge is less than 3000 pounds is 26%.