Answer:
P = 120*(
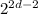 )
)
P(8) = 1, 966, 080
Explanation:
Since the population quadruples each day, the population for the subsequent day would be 4*(population of the previous day).
Thus, the evolution of the population value takes the form of a geometric progression, with a common ratio, r = 4
The n-th term of a geometric progression is given by:
 =
=
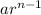 (1)
(1)
Where a is the 1st term of the progression.
From (1), our population would generally take the form:
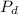 =
=
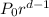 (2)
(2)
In this case, the initial value (1st term)
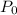 = 120.
= 120.
So putting r and
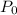 into (2):
into (2):
P(d) = 120*(
 )
)
Noting that 4 = 2²:
P(d) = 120*(
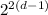 )
)
P(d) = 120*(
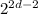 )
)
FOR d = 8:
P(d) = 120*(
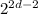 )
)
becomes:
P(8) = 120*(
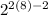 )
)
P(8) = 120*(
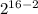 )
)
P(8) = 120*(
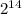 )
)
P(8) = 120*(16,384)
P(8) = 1, 966, 080