Answer:
a) 0.5 seconds and 3.5 seconds.
b) 5.98 seconds (2 d.p.)
c) No.
d) 254 feet at 2 seconds.
Explanation:
Given equation:
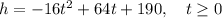
where:
- h is the height (in feet).
- t is the time (in seconds).
Part a
To calculate when the object will be 218 feet above the ground, substitute h = 218 into the equation and solve for t:

Therefore, the object will be 218 feet about the ground at 0.5 seconds and 3.5 seconds.
Part b
The object strikes the ground when h is zero. Therefore, substitute h = 0 into the equation and solve for t:
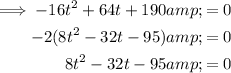
Use the quadratic formula to solve for t:
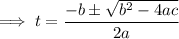
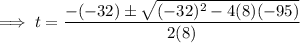
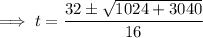


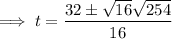
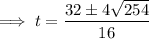
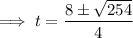
As t ≥ 0,
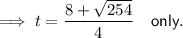

Therefore, the object strikes the ground at 5.98 seconds (2 d.p.).
Part c
To find if the object will reach a height of 300 feet above the ground, substitute h = 300 into the equation and solve for t:
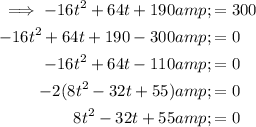
Use the quadratic formula to solve for t:
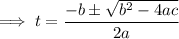

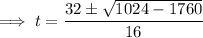

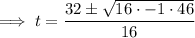
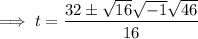
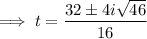
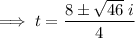
Therefore, as t is a complex number, the object will not reach a height of 300 feet.
Part d
The maximum height the object can reach is the y-coordinate of the vertex.
Find the x-coordinate of the vertex and substitute this into the equation to find the maximum height.

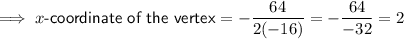
Substitute t = 2 into the equation:
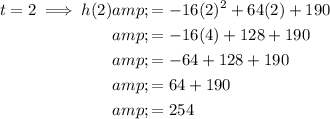
Therefore, the maximum height of the object is 254 feet.
It takes 2 seconds for the object to reach its maximum height.