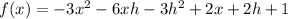Answer:
Option C,
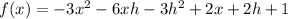
Explanation:
Oooo the ol canvas quiz yeesh.
Anyway, for this sort of problem, anywhere in your second equation that you see an x, sub for (x+h).
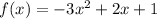
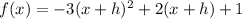
You must foil the first part
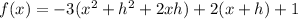
Now distribute to eliminate the parentheses
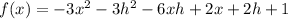
As your answer choice has it: