Answer:
x = ± 3
Explanation:
given y varies as
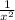 , then
, then
y = k ×
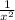 =
=
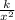 ← k is the constant of variation
← k is the constant of variation
to find k use the condition x = 2 , y = 1
1 =
 =
=
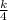 ( multiply both sides by 4 )
( multiply both sides by 4 )
4 = k
y =
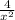 ← equation of variation
← equation of variation
when y =
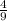 , then
, then
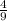 =
=
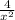 ( cross- multiply )
( cross- multiply )
4x² = 36 ( divide both sides by 4 )
x² = 9 ( take square root of both sides )
x = ±
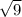 = ± 3
= ± 3