Question

Suppose the graph of

y
=
f
(
x
)
is stretched vertically by a factor of
3
, reflected across the
x
-axis, then translated left
7
units, and up
2
units.

The new graph will have equation y=

Answer 1

`y=-3(x+7)+2`

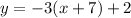
Explanation:

Alright, so the first mistake people make is to try to visualize this graph. For the sake of the problem, it does not matter in the slightest.

To start, we have y=f(x).

The first change is a vertical stretch. These are represented outside the parentheses. Meaning, the new stretched equation would be y=3(x). The three does not replace the "f", just no one would write the f into the equation as it is implied.

Next, the graph is reflected across the x-axis. This means that there is a negative outside of the parentheses. The new equation would be -3(x). As stretches are always greater than 1 and shrinks are between 0 and 1, it is clear the negative denotes a reflection.

Translations to the left are denoted as positives inside parentheses. In this case, left 7 would be -3(x+7).

Finally, upwards translations are positive numbers shown following the parentheses. Up two would make your final equation -3(x+7)+2.