Question

Show all work to identify the asymptotes and state the end behavior of the function f(x) = 6x/ x - 36

Answer 1

Vertical asymptotes are when the denominator is 0 but the numerator isn't 0.

`x-36=0 \implies x=36`

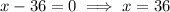
Since this value of x does not make the numerator equal to 0, the vertical asymptote is
`x=36`.

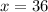Horizontal asymptotes are the limits as
`x \to \pm \infty`.

`\lim_(x \to \infty) (6x)/(x-36)=\lim_(x \to \infty)=(6)/(1-(36)/(x))=6\\\\\lim_(x \to -\infty) (6x)/(x-36)=\lim_(x \to -\infty)=(6)/(1-(36)/(x))=6\\\\`

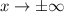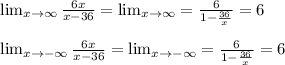
So, the horizontal asymptote is
`y=6`.

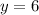End behavior:

• As
  `x \to \infty, f(x) \to -\infty`
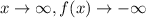
• As
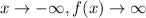  `x \to -\infty, f(x) \to \infty`.