Answer:
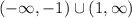
Explanation:
The function is always positive when it has a positive leading coefficient (since that means the graph will open up), and when the discriminant is negative (meaning the graph will never cross the x-axis).
Condition I. Leading coefficient is positive
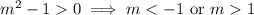
Condition II. Discriminant is negative
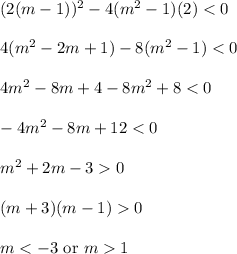
Taking the intersection of these intervals, we get
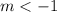 or
or
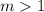 .
.