Answer: 11.5% (choice B)
=====================================================
Step-by-step explanation:
mu = 500 = mean
sigma = 100 = standard deviation
We'll need the z score for x = 620
z = (x - mu)/sigma
z = (620-500)/100
z = 1.20
The task of finding P(x > 620) is equivalent to P(z > 1.20)
Use a Z table or a Z calculator to find that
P(Z < 1.20) = 0.88493
which leads to
P(Z > 1.20) = 1 - P(Z < 1.20)
P(Z > 1.20) = 1 - 0.88493
P(Z > 1.20) = 0.11507
This converts to 11.507% and rounds to 11.5%
About 11.5% of the students score higher than a 620 on the SAT.
-------------------------
Another approach:
Open your favorite spreadsheet program. The command we'll be using is called NORMDIST. The template is this
NORMDIST(x, mu, sigma, 1)
- x = 620 = critical value
- mu = 500 = mean
- sigma = 100 = standard deviation
- The 1 at the end tells the spreadsheet to use a CDF instead of PDF. Use 0 if you want a PDF value.
If you were to type in
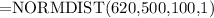 then you'll get the area under the normal distribution to the left of x = 620
then you'll get the area under the normal distribution to the left of x = 620
This means
 will get us the area to the right of 620. The result of that calculation is approximately 0.11507 which leads to the same answer of 11.5% as found earlier.
will get us the area to the right of 620. The result of that calculation is approximately 0.11507 which leads to the same answer of 11.5% as found earlier.
When using a spreadsheet, don't forget about the equal sign up front. Otherwise, the spreadsheet will treat the input as text and won't evaluate the command.
-------------------------
Another option is to use a TI83 or TI84 calculator.
Press the button labeled "2nd" in the top left corner. Then press the VARS key. Scroll down to "normalcdf"
The template is
normalcdf(L, U, mu, sigma)
- L = lower boundary
- U = upper boundary
- mu = mean
- sigma = standard deviation
The mu and sigma values aren't anything new here. But the L and U are. In this case L = 620 is the lower boundary and technically there isn't an upper boundary since it's infinity. Unfortunately the calculator wants a number here, so we just pick something very large. You could go for U = 99999 as the stand in for "infinity". The key is to make sure it's more than 3 standard deviations away from the mean.
So if you were to type in
 then the calculator will display roughly 0.11507, which is in line with the other answers mentioned earlier.
then the calculator will display roughly 0.11507, which is in line with the other answers mentioned earlier.
As you can see, there are many options to pick from. Searching out "normal distribution calculator" or "z calculator" will yield many free options. Feel free to pick your favorite.