Question

Suppose the sequence 28, 14, ... is geometric.

a)Determine the common ratio.

b) List the next 3 terms in the sequence. Explain your reasoning.


please help me!!

Answer 1

⇒In a geometric sequence to find the common ratio(r) we use the formula

`r=(T_(2) )/(T_(1) )`

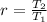
But in general we use the formula is
`r=(T_(n+1) )/(T_(n) )`

In this case we are going to use

`r=(14)/(28) \\r=(1)/(2)`

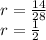
⇒The common ratio of the sequence is
`(1)/(2)`, to get the 3 consecutive terms you are going to multiply the current term by the common ratio which in this case is
`(1)/(2)`

`T_(3) =T_(2) * r\\\\T_(3)=14((1)/(2) )\\T_(3) =7`

`T_(4) =T_(3) *r\\T_(4)=7((1)/(2) )\\T_(4)=(7)/(2)`

`T_(5)=T_(4) *r\\T_(5)=(7)/(2) *(1)/(2) \\T_(5)=(7)/(4)`

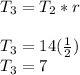
If you have any questions ask me as soon as possible.

GOODLUCK!!

Answer 2

see explanation

Explanation:

(a)

common ratio r =
`(a_(2) )/(a_(1) )` =
`(14)/(28)` =
`(1)/(2)` = 0.5

(b)

to find the next term, multiply the previous term by r = 0.5

14 × 0.5 = 7

7 × 0.5 = 3.5

3.5 × 0.5 = 1.75

the next 3 terms in the sequence are 7 , 3.5 , 1.75