Question

determine the inverse function of f(x) = x² + x - 6, x> - 1/2, if it exists. Then, state its domain and range. ​

Answer 1

Since the domain is restricted to one side of the axis of symmetry of the full graph of f(x), an inverse does exist.

Letting
`f(x)=y`,

`x=y^2 +y-6\\\\x=\left(y+(1)/(2) \right)^2 -(25)/(4)\\\\x+(25)/(4)=\left(y+(1)/(2) \right)^2`

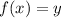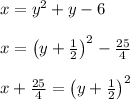
Since the domain is restricted to the right hand side of the axis of symmetry, and since the range of the inverse is the same as the domain of the original function, we take the positive square root.

`\sqrt{x+(25)/(4)}=y+(1)/(2)\\\\y=f^(-1)(x)=\sqrt{x+(25)/(4)}-(1)/(2)`

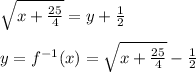
The domain of the inverse is the range of the original function, which is
`\left[-(25)/(4), \infty \right)`.

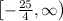The range of the inverse is the domain of the original function, which is
`\left[-(1)/(2), \infty)`,