Question

A rectangle is shown below.

measurements are to the nearest cm.
17 cm
9 cm
Calculate the lower bound for the area of the rectangle.
Calculate the upper bound for the perimeter of the rectangle

Answer 1

lower bound for area = 140.25 square cm

upper bound for perimeter = 54 cm

======================================================

Step-by-step explanation:

L = length

W = width

The unknown length L is rounded to the nearest cm to get to 17

This means it's in the interval
`16.5 \le L < 17.5`

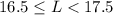
The smallest it can get is L = 16.5 since that rounds to 17

It doesn't reach 17.5 since that would round to 18. But it could be L = 17.49 or L = 17.499 or L = 17.4999 and so on.

Similarly, if the unknown width W rounds to 9 cm, then its unrounded value is somewhere in the interval
`8.5 \le W < 9.5`

------------------------

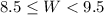
Select the lower bounds of L and W to compute the lower bound of the area

length*width = L*W = 16.5*8.5 = 140.25

The smallest area possible is 140.25 square cm.

--------------------------

Use the upper bounds of each L and W to find the upper bound of the perimeter.

P = 2(L+W)

P = 2(17.5 + 9.5)

P = 54

In the previous example, we could have a true area of 140.25 square cm. However in this case, there's no way to reach this upper bound 54 itself. This is the so called "ceiling" which we can think of as an electric fence or asymptote value.

We could have the following example perimeter values that approach 54 but not actually reach it

• perimeter = 53.9
• perimeter = 53.99
• perimeter = 53.999
• perimeter = 53.9999

and so on.