Answer:
- Vertex = (-3, -1).
- y-intercept = (0, 2).
- x-intercepts = (-2, 0) and (-4, 0).
- Domain = (-∞, ∞).
- Range = [-1, ∞).
Explanation:
Given absolute value function:
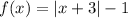
The parent function of the given function is:
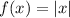
Graph of the parent absolute function:
- Line |y| = -x where x ≤ 0
- Line |y| = x where x ≥ 0
- Vertex at (0, 0)
Translations
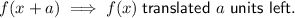



Therefore, the given function is the parent function translated 3 units left and 1 unit down.
If the vertex of the parent function is (0, 0) then the vertex of the given function is:
⇒ Vertex = (0 - 3, 0 - 1) = (-3, -1)
To find the y-intercept, substitute x = 0 into the given function:
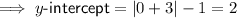
To find the x-intercepts, set the function to zero and solve for x:
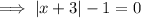
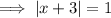
Therefore:
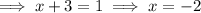
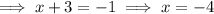
Therefore, the x-intercepts are (-2, 0) and (-4, 0).
To sketch the graph:
- Plot the found vertex, y-intercept and x-intercepts.
- Draw a straight line from the vertex through (-2, 0) and the y-intercept.
- Draw a straight line from the vertex through (-4, 0).
- Ensure the graph is symmetrical about x = -3.
Note: When sketching a graph, be sure to label all points where the line crosses the axes.
The domain of a function is the set of all possible input values (x-values).
The domain of the given function is unrestricted and therefore (-∞, ∞).
The range of a function is the set of all possible output values (y-values).
The minimum of the function is the y-value of the vertex: y = -1.
Therefore, the range of the given function is: [-1, ∞).