Question

Find an equation in the form y=mx + b

Answer 1

A)
`y = (1)/(10)x + 28`

B) $116.5

Explanation:

The data we are given is:

• for 440 minutes of usage, the total cost is $72

• for 940 minutes of usage, the total cost is $122

A)

In order to find an equation in the form
`y = mx + b`, we must first express the given data as coordinates in the form
`(x, y)`.

We are told that
`x` is the number of monthly minutes, and
`y` is the total monthly fee. Therefore the first piece of data expressed as coordinates is (440, 72), and for the second piece of data, it is (940, 122).

Now that we have the coordinates, we can make an equation using the formula:

`\boxed{(y - y_1)/(y_2 - y_1)= (x - x_1)/(x_2 - x_1)}`,

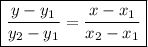where
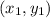`(x_1, y_1)` is (440, 72) and
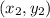`(x_2, y_2)` is (940, 122).

Substituting the values into the formula, we get:

`(y - 72)/(122 - 72)= (x - 440)/(940 - 440)`

⇒
`(y - 72)/(50) = (x - 440)/(500)`

⇒
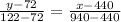
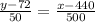
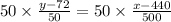`50 * (y - 72)/(50) =50 * (x - 440)/(500)` [Multiplying both sides of the equation by 50]

⇒
`y - 72 = (x - 440)/(10)`

⇒
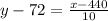
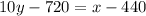`10y - 720 = x - 440` [Multiplying both sides by 10]

⇒
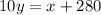`10y = x +280` [Adding 720 to both sides]

⇒
`y = (1)/(10)x + 28` (Answer)

B)

To find the total cost if 885 minutes are used, we have to replace
`x` in the above equation with 885:

`y = (1)/(10)(885) + 28`

⇒
`y = 88.5 + 28`

⇒
`y = 116.5`

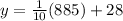
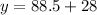
Therefore, the total cost will be $116.5. (Answer)